


This will allow us to transform scores in any numeric dataset, using any scale, into a standard metric. In this chapter, we will learn how to use the statistics of the mean and standard deviation to generate standard scores, or Z-scores.
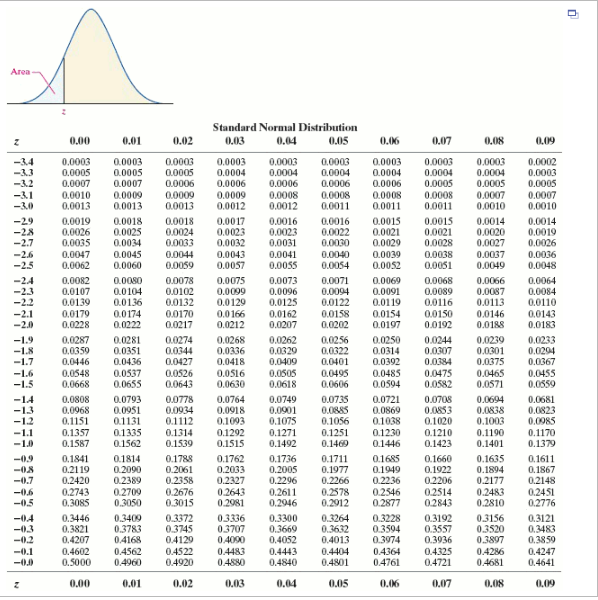
The same is true of trying to compare numbers from different datasets. In fact, if you are a native speaker of English, you might have heard before “that’s like comparing oranges to apples,” meaning it’s impossible to compare. One is more tart, the other quite mild in flavour, so it is difficult to compare oranges and apples. Why? When we think about it, it is tough to directly compare them in terms of the property of sweetness. How sweet are these fruits? Is an apple sweeter? Or is an orange sweeter? What do you think? Is it difficult to say? Usually when I survey people with this question, there is a pretty even split, with half saying an apple is sweeter, and the other half saying the orange is sweeter. “Oranges” by Dious is marked with CC PDM 1.0 Have a look at these images: “Apple” by Open Grid Scheduler / Grid Engine is marked with CC0 1.0 In this chapter, we will address the topic of Z-scores, one type of what are commonly called standard scores.īefore we begin, we will examine a real world example of why standardizing scores is useful and important. This curve is defined by the probability density function $$\phi(x)=\frac\phi(x)dx.3. In your question, you state that $P(z\geq 3.9)= 0.000048$-this is that very small area ABOVE the $z$ score.Ĭonsider the following picture, the $P(z3.16)$ should be, but could not shade it in because, well, it is quite small!īut how are $z$-scores calculated? As stated, it is the area below the Normal distribution's curve. There does exist a very small amount of area (again, synonymous with probability) above $3.16\sigma$. The probability is the area below the Normal distribution's curve.įor a score of $z=3.16$, the area under the Normal distribution from $-\infty \sigma$ to $3.16\sigma$ is $\approx 1$ (this is the probability). You said anything $>z=3.16$ will have a probability = 1. Recall that a $z$-score is simply the number of standard deviations away from the mean ($\mu$).


 0 kommentar(er)
0 kommentar(er)
